The contextual revolution (don’t really know if that’s a thing, but it sounds official) emerged in the MLB the past few years, attempting to control for more situational effects than current sabermetric driven baseball stats. These models build upon Bill James’s work, Tom Tango’s all-important linear weights, and similar metrics that account for league, park, and positional production.
Baseball Prospectus (BP) writers developed baseball statistics that further quantify performance using mixed models . You can find a good introduction to mixed models in this article written by Jonathan Judge, Harry Pavlidis and Dan Brooks of BP, but if you are familiar with linear or logistic regression, a mixed model attempts to estimate the average performance over the course of the season (fixed linear model) and use the residuals (or error) to simultaneously quantify the contributions of ”random” participants in any given play. Now why do I say random? It isn’t so much that these participants are random, but that the baseball players are always changing and the number of “random” interactions they have throughout a season is endless, while the effect of an 0-2 count on run production says relatively consistent or fixed throughout a whole season.
Some existing baseball stats based on mixed models include:
- Called Strikes Above Average (CSAA) – defensive statistic that measures catcher framing skills controlling for the batter, pitcher, catcher, and umpire
- Swipe Rate Above Average (SRAA) – base running metric that attempts to quantify base stealing ability for batters, and stolen base prevention for pitchers and catchers
- Take Off Rate Above Average (TRAA) – player specific effects on base stealing attempts
- cFIP – a new version of Fielding Independent Pitching (FIP) taking into account many aspects of a plate appearance. Read more about it here.
By the title you can probably guess this article is about stolen bases, and you are correct. Specifically, I will be discussing Swipe Rate Above Average or SRAA for short. SRAA is derived from a mixed model that attempts to account for the inning, the stadium, the quality of the pitcher, and the pitcher, catcher, and lead runner involved. SRAA is directly derived from a player’s random effect and is a single number generally ranging from -10% to 10% describing the additional probability a player contributes to a successful steal. For example, Mike Trout had a 4% SRAA in 2016. Given the average stolen base situation, Trout is 4% more likely to successfully steal than the average baserunner in 2016.
While SRAA accounts for pitcher skill using cFIP1, the quality of a pitcher can’t necessarily control for all variation in a pitcher’s pitch sequence or the occasional mistake in the dirt. Pitches in the dirt, pitchouts2, off-speed, and fastballs are treated equally in SRAA. Consequently, SRAA values may be lacking for runners that disproportionately get thrown out on pitchouts or for catchers that consistently block balls in the dirt while still throwing out the runner.
Lets explore some evidence of these effects before we include them in the pitch adjusted (pSRAA) model. I started by subsetting Retrosheet play-by-play data from the 2016 season to only stolen base attempts by lead runners. For example, events with a steal of second base with a man on third were not included. I only included situations where a pitch preceded a stolen base attempt. I supplemented the play-by-play data with PITCHf/x data which tracks trajectories of every pitch in the MLB. I aligned the pitch data with each stolen base with minimal missing connections between the two datasets3 and ended up with 2,809 total attempts. Excluding some of these stolen bases means for those who are familiar with SRAA, my SRAA numbers will not match up directly with BP’s numbers.
I first examined pitch speed and its effects on stolen base percentage. It’s no surprise that in 2016 runners succeed more often on slower pitches.
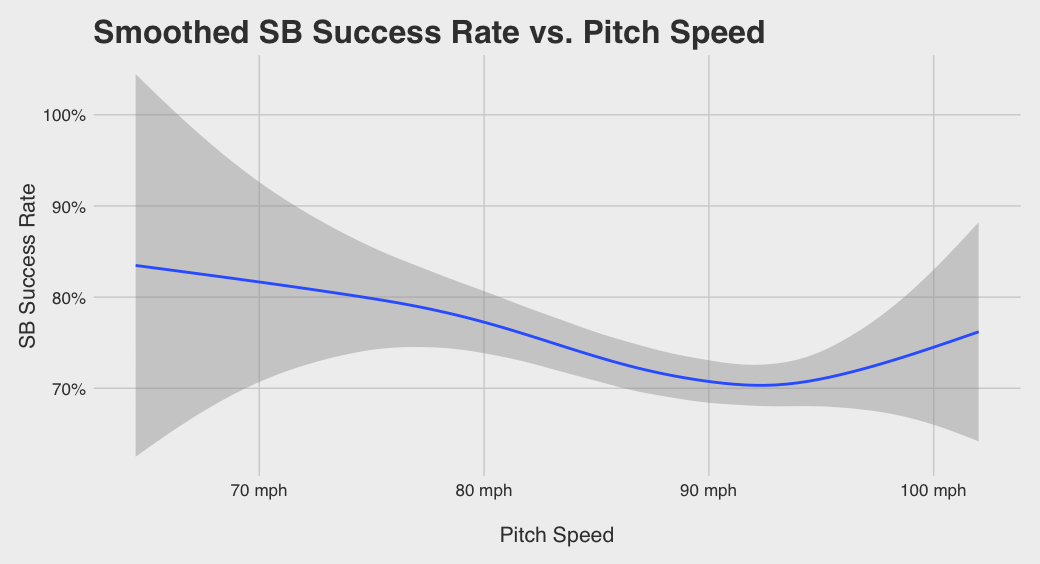
Notice a slightly higher success rate for pitch speeds that fall above 95 mph. This phenomenon is not unique to 2016, and Jeff Sullivanhypothesized that good base stealers are the ones stealing against fireballers. Indeed, while only 8% of stolen bases occur during a pitch that is 95 mph or higher, speedsters Billy Hamilton and Starling Marte attempted over 12% of their stolen bases in these situations. These situations tend to arise later4 in closer games5 meaning base stealers ought to be more certain of success before attempting to steal.
In addition to pitch speed, we also have access to pitch location data through PITCHf/x. As you can see in the figure below, the SB probability varies more drastically by location, and therefore, is the most meaningful of the two pitch metrics. The results below mirror the results I would expect. High SB probability along the right side of the plate for left-handed hitters confirms that most catchers (if not all) are right-handed which makes it hard to throw over left-handed hitters. Similarly, catchers have more success with right-handed hitters and pitches closer to their throwing shoulder. And finally, the most obvious of all: it’s hard to throw a runner out when the ball hits the ground.
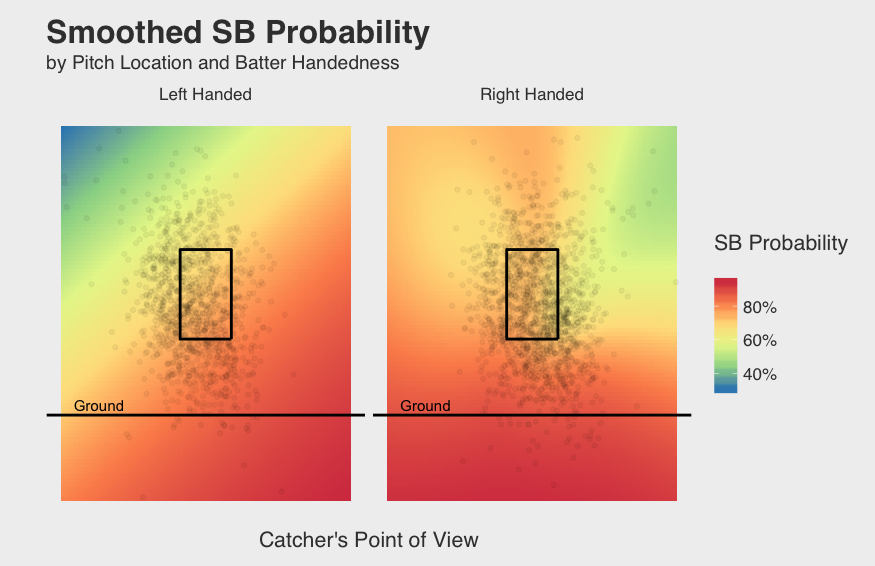
I also included the PITCHf/x pitch descriptions since they help improve the model slightly. Some descriptions occurred only a few times, so I combined them into larger categories:
- Dirt: Ball in Dirt, Swinging Strike (Blocked)
- Pitchout: Pitchout, Swinging Pitchout
- Strike/Ball: Ball, Called Strike,
- Swinging Strike: Foul Tip, Missed Bunt, Swinging Strike
Below is a table detailing the SB success rates in each of the four groups. Dirt and Pitchout are the most extreme categories with “normal” pitches falling in-between. Something that jumped out at me was the lower success rate on swinging strikes, as I would expect this to distract the catcher. Two explanations I can come up with are: 1) catchers tend to hold the no-swing pitches a split second longer to get the call from the ump, or 2) swinging pitches occur during a hit and run6 play where runners tend to be less skilled at stealing bases.
| Pitch Description | SB% | Number of Attempts |
|---|---|---|
| Dirt | 87.8% | 197 |
| Strike/Ball | 74.2% | 2042 |
| Swinging Strike | 63.7% | 534 |
| Pitchout | 33.3% | 36 |
Controlling for the lead runner’s base is the last addition I made to the original SRAA model. Adding this effect improved the model (AIC to be specific), indicating runners stealing third were more likely on average to be successful than runners attempting to steal second and especially home. A likely explanation is that runners stealing third need to be more confident in their ability to steal in the current situation and have a right-handed hitter obstructing the catchers throw about 65% of the time.
So now that we have this new metric pSRAA, lets take a look at how it deviates from SRAA. As you can see in the figure below, the distribution of both metrics are fairly similar.
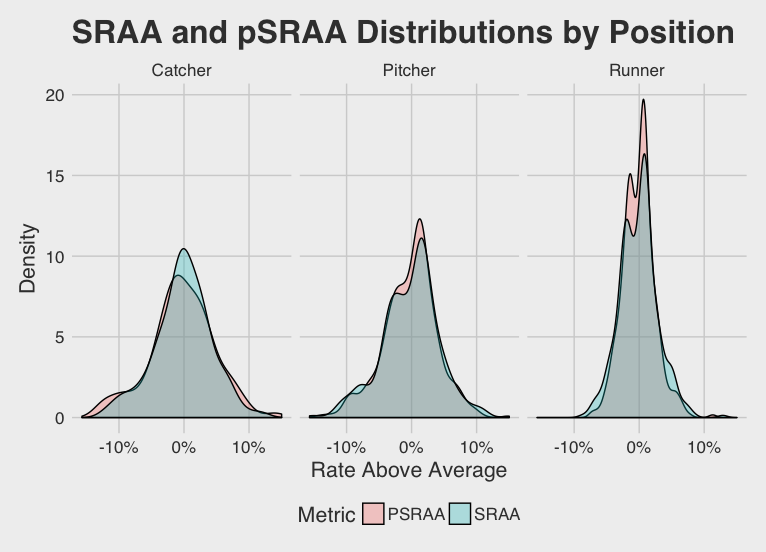
pSRAA has a slightly tighter distribution for pitchers and runners, meaning pSRAA has absorbed some of the expected SB probability in these new variables and pushed pitcher and runner SB skills closer to the mean. This phenomenon occurs most likely because the variables we are trying to control for are largely out of control for these players and are not rectifiable or exploitable. By that I mean, pitchers can’t control whether the one pitch they throw in the dirt happens to coincide with a runner taking off, but catchers can use this event to prove their skill. While a pitcher “loses control” of the SB situation when the ball is released, a catcher can make a brilliant play, saving a potential wild pitch and converting it into an out. Thus, we see a wider variation in pSRAA for catchers, as pSRAA identifies the increasingly elite talent and the replacement players that struggle to nab runners on pitchouts.
Examining how players’ metrics improved or worsened after controlling for these additional effects reveals some drastic changes, but mostly small adjustments. The figure below illustrates the change from the old metric to the new metric. The closer a player is to the dotted line (pSRAA = SRAA), the less that player deviated from the original SRAA measure. If a player ends up above this line, it means that pSRAA is higher than SRAA, so when controlling for pitches, pSRAA attributes more success (for runners — less success for pitchers and catchers) to their ability rather than luck.
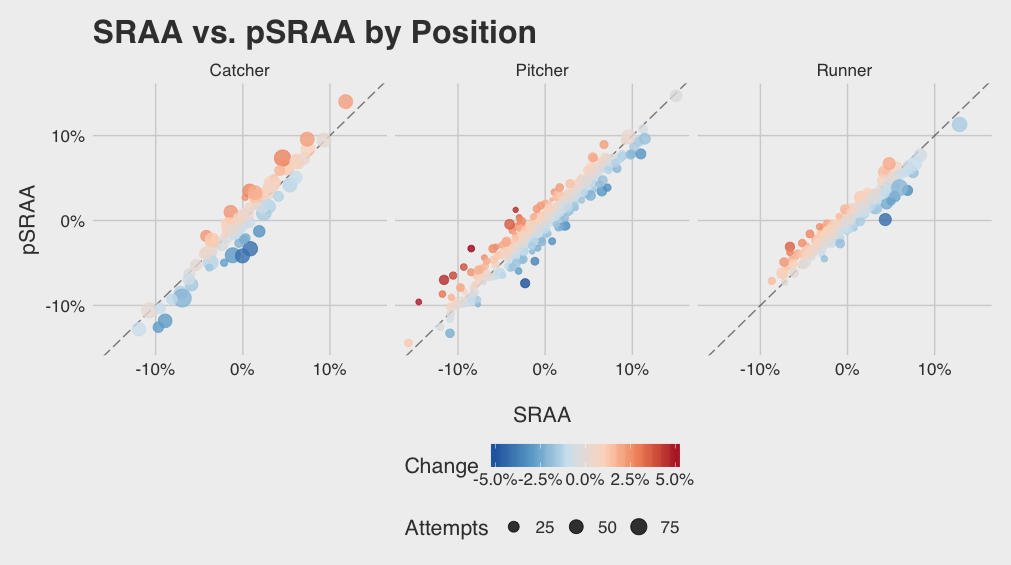
How does this new pSRAA model help us as baseball fans or analysts? pSRAA can identify where SRAA was under or overvaluing players’ skills. For example, SRAA undervalues catcher Chris Iannetta at a 0.86% SRAA when pSRAA pegs him at whopping -4.19% (negative is good for catchers)! In other words, Iannetta jumps from the 43rd percentile of catchers to the 70th percentile!
To give you an idea of the kind of adjustments pSRAA makes, below is a sample stolen base attempt against Iannetta (video has no sound for those of you who are watching at work; for sound go to 1:51:40 here), specifically a SB attempt that the model predicts will happen 85.5% of the time. Actually, it is more like 88.4% if you account for the runner, Lorenzo Cain, the 15th fastest baseball player according to Statcast’s speed measure.
Now lets just freeze that frame. The ball is almost on the ground, and not to mention, only thrown at 80 mph, giving Cain almost an extra tenth of a second to get to second base. Regardless, Iannetta guns him out with an impeccable throw.

Not only can we use pSRAA to uncover insights such as above, but we can also abuse pSRAA to easily find awesome plays like this top 5 play below. J.T. Realmuto, known for his unbelievable pop time, throws out Ben Revere on this gem of a play. The pSRAA model gives Realmuto a 10% chance of throwing out Ben Revere, but Realmuto pops up in a staggering 1.78 seconds (via Statcast) and throws a perfect 85 mph toss to second. Be careful, I left the sound on for this one so you can hear the short-hop as he picks the throw in the dirt.
Or this scenario which had a 92% stolen base probability (sound again). A.j. Pierzynski picks a throw off the ground, navigates around Brandon Phillips to beat Suarez by a mile.
And finally, here is an example of a successful stolen base the model predicts will happen 15% of the time —not a surprise when you see where the pitch is thrown (actually 43% when you account for the speedy Rajai Davis and the way below average Kurt Suzuki)
pSRAA does well for these purposes, but may not illustrate the total value a player adds to his team’s success. A runner with a high pSRAA value with only a couple stolen base attempts hasn’t added much value to his team since he didn’t utilize his skill often enough. We can leverage pSRAA and stolen base/caught stealing (CS) run values to come up with a more useful metric, which I have aptly named Pitch Adjusted Swipe Rate Runs Above Average (pSRrAA) —a mouthful, I know. I based pSRrAA upon linear weights metrics like FanGraphs Weighted Stolen Base Runs (wSB). The term linear weights, often used in the world of baseball statistics, translates to the average run value of a certain action and its effect on run scoring over the course of an inning. For example, lets say there is a man on first base with no outs. The average number of runs scored in an inning in 2016 starting with this exact situation is 0.8744 runs. He gets caught stealing, and now the situation is nobody on and 1 out. Starting in this situation, the run expectancy drops to 0.2737. Thus, the value of this specific play was about -0.6 runs. Examining these situations over the course of the whole season leaves us with average run values that we can assign to SB and CS. Combining the run values for SB (runSB = .2 runs) and CS (runCS = -.41 runs) produced by FanGraphs for the 2016 season, we can use pSRAA to attribute the run values more accurately:
This method for calculating pSRrAA works because of the following:
- pSRRA already determines the probability a certain player adds to a SB above average.
- If a player adds 10% probability to a SB, they are contributing runSB 10% more than the average player and runCS 10% less.
- pSRRA x (runSB-runCS) quantifies the average attempt value, so then we just multiply by attempts to get a full run value over the course of the season.
Of course, as I alluded to in the beginning pSRAA doesn’t account for all types of stolen bases, only ones with pitches involved. Consequently, pSRrAA doesn’t account for the total value runners and pitchers contribute to their teams because attempts are excluded in which catcher isn’t involved. Finally, I will leave you with a table of the top 10 and bottom 10 performers for each position according to pSRrAA. And as always, you can find the code associated with pSRAA/pSRrAA and the analysis on my GitHub page here. Checkout my new Facebook page to stay up to date on new articles.
| Catcher | pSRAA | pSRrAA | Pitcher | pSRAA | pSRrAA | Runner | pSRAA | pSRrAA |
|---|---|---|---|---|---|---|---|---|
| Jonathan Lucroy | -9.13% | -5.52 | Drew Pomeranz | -13.3% | -0.97 | Billy Hamilton | 11.31% | 3.93 |
| Salvador Perez | -10.57% | -4.19 | Tom Koehler | -9.2% | -0.95 | Starling Marte | 6.72% | 2.01 |
| Welington Castillo | -12.80% | -3.75 | Wily Peralta | -6.2% | -0.8 | Rajai Davis | 7.69% | 1.78 |
| James McCann | -11.82% | -3.46 | Tyler Chatwood | -14.4% | -0.79 | Jonathan Villar | 3.87% | 1.7 |
| Jett Bandy | -8.49% | -1.97 | Ian Kennedy | -7.0% | -0.68 | Trea Turner | 6.70% | 1.39 |
| Buster Posey | -4.95% | -1.84 | Jaime Garcia | -7.4% | -0.68 | Eduardo Nunez | 4.15% | 1.11 |
| Martin Maldonado | -7.55% | -1.8 | Mike Fiers | -12.5% | -0.61 | Jarrod Dyson | 6.26% | 1.03 |
| Evan Gattis | -12.57% | -1.76 | Zach Davies | -6.2% | -0.61 | Odubel Herrera | 5.71% | 0.98 |
| J. T. Realmuto | -4.09% | -1.55 | Jon Lester | -3.0% | -0.6 | Mike Trout | 3.93% | 0.79 |
| Gary Sanchez | -10.35% | -1.45 | Justin Grimm | -11.0% | -0.53 | Keon Broxton | 6.10% | 0.78 |
| Catcher | pSRAA | pSRrAA | Pitcher | pSRAA | pSRrAA | Runner | pSRAA | pSRrAA |
|---|---|---|---|---|---|---|---|---|
| Hank Conger | 7.29% | 1.38 | Anibal Sanchez | 4.6% | 0.76 | Danny Santana | -3.09% | -0.3 |
| Russell Martin | 4.19% | 1.38 | Felix Hernandez | 8.7% | 0.8 | Rougned Odor | -3.11% | -0.3 |
| Francisco Cervelli | 4.31% | 1.82 | Jake Arrieta | 6.2% | 0.83 | Erick Aybar | -7.12% | -0.3 |
| Bobby Wilson | 6.94% | 1.82 | Gerrit Cole | 7.2% | 0.84 | Logan Forsythe | -5.02% | -0.34 |
| Travis d'Arnaud | 6.27% | 2.49 | Matt Andriese | 9.4% | 0.92 | Andrew McCutchen | -5.08% | -0.34 |
| Nick Hundley | 8.38% | 2.61 | Cole Hamels | 7.8% | 0.96 | Alexei Ramirez | -4.89% | -0.36 |
| Miguel Montero | 9.48% | 2.95 | Dellin Betances | 10.8% | 0.99 | Nori Aoki | -5.18% | -0.41 |
| Kurt Suzuki | 9.58% | 2.98 | Ubaldo Jimenez | 9.6% | 1.47 | George Springer | -4.90% | -0.48 |
| Derek Norris | 7.35% | 3.45 | Jimmy Nelson | 14.7% | 2.78 | Kirk Nieuwenhuis | -6.16% | -0.49 |
| Tyler Flowers | 14.00% | 4.27 | Noah Syndergaard | 9.9% | 2.95 | Cesar Hernandez | -6.20% | -1.02 |
Featured image by Keith Allison.
-
See above link for more information. ↩
-
A ball intentionally through high and outside to prevent stolen bases. ↩
-
Only 3 stolen bases did not have PITCHf/x data since there technically wasn’t a pitch that occurred (e.g., steal of third then steal home on a passed ball). An additional 8 did not have valid trajectory readings in PITCHf/x. ↩
-
About 1 inning later on average ↩
-
Stealing team is only .39 runs ahead rather than .46 runs ahead on average ↩
-
Attempt to hit the ball to draw middle infielders away from the base to help the runner advance ↩